Of all the chapters in this book, this one has the most powerful mathematics. That can mean that it is very demanding for
your students unless you make clear to them that it is the ideas conveyed and not necessarily the details of the developments
that are important. If you can point that out to them (probably many times) then they can come away with some understanding of
the power mathematics provides in analyzing complex situations.
One way you can help your students see the forest instead of just the local trees is by reviewing with them each day the
key points made in the chapter as they accumulate. I will list those points at the end of this chapter commentary.
Section Notes and Activities:Section 9.1 not only reviews integer powers but also exposes a new and significant role for binary representation. It significantly
shortcuts the calculation of high powers. This process will play a similar role in Section 9.3, when rational powers are
considered
Section 9.2 on square root offers you an opportunity to talk with your class about some pedagogical history. They have met that complicated
algorithm for finding square root back in Chapter 2 (and probably, like most of us, immediately forgot it!) Now they have this
version of Newton’s algorithm. It turns out that this algorithm became popular in the 1960s as a replacement for that earlier one.
Unfortunately, however, the 1960s was before the availability of calculators and the involved long division made that algorithm
obsolete. Remarkably, educators failed to adopt a third, simpler method of finding square roots, despite the fact that it should
have occurred to anyone seeking that value.
That third method is simply trial and error. Since square root and squaring are inverse operations, you can locate square roots
by squaring candidates. For example, to find the square root of 5, 22 = 4 and 32 = 9 tell
us that the root is between 2 and 3. 2.52 = 6.25 is still too high, so we can try 2.3: 2.32
= 5.29 is getting close and 2.22 = 4.84 tells us that the answer is between
2.2 and 2.3. Now we can try 2.25, either to round our answer or to seek additional decimal places. Granted that this requires
multiplication, but for most of us multiplication is preferred to division.
Interestingly, this method never caught on even with the introduction of simple calculators. And there is a reason for this.
Almost all of the early calculators included a square root key along with one for adding, subtracting, multiplying and dividing.
The reason for that: programming Newton’s algorithm is very simple and thus it was simple to include it.
Sharing some of that history with your students should give them appreciation for their access to calculation.
Section 9.3 on rational and real powers uses a similar binary trick used to shortcut integer powers to calculate roots. While you can serve
your students by working through one of these calculations to show how they are done, the idea here is to show them how a complex
operation is carried out, not to have them master this procedure. As you work through such an example with them, it will serve them
if you point out how the rules for multiplying exponents serves them here.
It is worth pausing as students address this section to remind them that exponents can easily be translated into integer powers
and roots. For example, 52.5 is equivalent to 52 • 51/2 =
25 times the square root of 5 and 71.3 =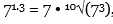 
which is 7 times the tenth root of 7 cubed.
Section 9.4 on exponents and logs is one of the longest in this text and there is a great deal of content in it. Today, however, most of this
chapter is only of historic interest and you can show what was involved with a few simple examples or even skip it entirely. Today’s
use of logs begins at the end of page 234.
Section 9.5 introduces the extremely important differential equation y’ = ky and its equivalent equation y = Cekx. This is
heady (and stressful) material for these students, so you will probably want to focus on how the ideas work with help from the panels.
The central idea is powerful and, as the examples and exercises suggest, quite pervasive. If you can show your students how to work a
few of the exercises, you will have given them quite a bit of scientific power.
Section 9.6 on logistic growth provides a necessary panacea for out-of-control exponential growth. Unless you are careful, this section will
seem like piling on the piling on of Section 9.5. Instead, you can focus their attention on the added factor (1 – P/L) and
its effect.
Here are the central ideas of this chapter.
1. The rules for powers are very general: xπ * xe = xπ+e
2. Binary numbers are useful in ways other than the representation and processing of decimal numbers.
3. Square root, because it is simple to calculate (by a computer) and involves two, has a special role in calculating other roots.
4. Today the role of logarithms is to serve as an inverse function for exponentiation.
log 10x = x and ln ex = x. Note how these appear on the calculator as inverses of log and
ln keys.
5. Whenever you have a rate of change of some quantity dependent on how much of that quantity is available, the result is
exponential growth.
6. Like the Fantasia episode, exponential growth, because it increases faster and faster, soon gets out of hand. To counter this,
we, or often Mother Nature, apply brakes resulting in the logistic equation. Graphically this effect changes a graph that swoops
up forever into a flattened off curve as that limiting factor applies.