About Mathematics Commentary
Chapter 2. Algorithms, Functions and Equations
What this chapter is aboutThis chapter reviews some concepts and notation from school mathematics that will be familiar to these students and of use
in much of what will follow. While the concepts may be familiar, the examples used to illustrate them will almost certainly be
unfamiliar to many of them. Of the three — algorithm, function and equation — the one with which students will probably be
least familiar is the first: algorithm. Whether they have used the term or not, most students will have applied many algorithms
(as set step-by-step procedures, usually memorized.)
The real point of this chapter, however, is that mathematical procedures like algorithms are not heaven-sent, but are based
on the underlying structure of mathematics. That is, there is a “Why?” behind each of the steps whose answer is more important than
the steps themselves.
Section Notes and ActivitiesSection 2.1 Here the algorithm that enters numbers in a calculator leads to synthetic substitution, a useful tool with many applications.
Central to this development is interpreting a polynomial right-to-left and left-to-right. That we interpret numbers from right to
left is made evident, as the text points out, when you ask what values the left-hand digits in numbers like 5,268,433,207 contribute.
Even with the commas inserted (as they are not in the text) to see that the 5 represents 5 trillion, it is necessary to see the
number right-to-left. One way to display this is to hide the rightmost digits of a large number and ask what are the digit values
that still appear.
The left-to-right representation of a polynomial
is confusing to some students, and that is what makes synthetic substitution such a useful tool. Carefully “simplifying” the
right member of that equation is important and it is useful to compare that simplification with numerical examples like
Note: Decimal values between zero and one are interpreted left-to-right. To determine the value of 5 in .192305, you need to see
its location in relation to the decimal point, as hiding some of the intermediate digits would make clear. To fit the right-to-left
approach that number would have to be interpreted as 192305·10-6. We recommend that you avoid this possible confusion unless a
student raises the question.
Section 2.2 is designed to show how a complicated algorithm that was taught by rote — do this, then do this,… — can be justified by both
geometric and algebraic means. (GR: As a beginning teacher in the 1940s I taught this rote algorithm as part of my 8th grade arithmetic
course of studies. Like my students, at that time I had no idea why the process worked. ES: I had the same experience in the 1960s.)
One way of approaching this algorithm is to treat it as a trick: here is a way to calculate square roots without a calculator
another item that will be unfamiliar to their STEM classmates. Another is to treat it as a historical artifact: Your grandparents
probably had to learn this. (Be happy things have changed.)
This algorithm has a role to play later in comparison with Newton’s Method for square root extraction, when that process is
introduced in Chapter 9.
Section 2.3 is a standard introduction to functions and function notation. The idea of a function as a kind of black box will probably be
familiar to many of your students from their earlier school
experiences, but you may want to illustrate with a few examples such as: 
If you have a programmable calculator, you can write simple programs to provide such clues. You could, for example, enter a
program labeled TEST with the three steps Input X, X^2 – 1, store Y, Display Y. That program represents the first example of the
previous paragraph. To change programs, you need only modify that second step. Using such calculator-based programs gives students
a sense of the function as a processing tool.
You might also remind the students that functions in science can be useful even when there is no simple mathematical equation
running them. For example, in developing a drug, a medical lab needs to find a relationship between the dosage and the effect.
An airline manufacturer seeks to relate how much fuel is used at different speeds and altitudes. These relationships may be conveyed
by tables or graphs rather than equations.
Section 2.4 shows how a computer can solve equations by seeing where the corresponding function crosses the x-axis. Of course, when a function
graph crosses the x-axis, the value of f(x) = 0, and that x is the equation solution.
A nice trick at the top of page 34 is employed to determine when f(x) = 0 in an interval. Where f(x) crosses the x-axis the value
of f(x) changes sign and a sign change takes place when the product of f(x) below and f(x) above is negative. What is nice about this
trick is that it makes use of a basic rule for integer multiplication in a new setting. This is worth pointing out to your students.
There are, of course, problems with this trick. The graph might not cross and simply be tangent. And the graph might cross twice
in an interval. These cases must be considered in a full program, but the basic algorithm works for most functions. An important feature
of algorithms is how unforgiving they are as anyone who has done computer programming can attest.
As a class demonstration of the techniques of this chapter, you could use Panel 2.1.2 (the panel that carries out synthetic
substitution to produce polynomial function values) to find a positive root of the equation 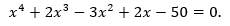
For the corresponding function 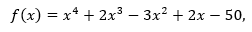 the panel gives (0,-50), (1,-48), (2,-26) and (3,64). Thus the root lies between x = 2 and x = 3. Now you can try x = 2.5, etc.
Once you have found a root to, say, two decimal places, you can compare your result with Panel 2.4.1.
the panel gives (0,-50), (1,-48), (2,-26) and (3,64). Thus the root lies between x = 2 and x = 3. Now you can try x = 2.5, etc.
Once you have found a root to, say, two decimal places, you can compare your result with Panel 2.4.1.
Chapter 2 is about algorithms and an algorithm supporting Panel 1.1.1 could serve as a
kind of summary activity; however, this could take an entire class session. If you are
uncomfortable doing it or, if you think it is inappropriate for your class, simply do not
do so. Or you might use just part of it to suggest how similar the steps are. If you do use
it, be sure you have the students provide each step along the way.
What is Going On in Panel 1.1.1The very first panel, Panel 1.1.1, should have served many purposes already. It served
as an introduction to the way panels work, giving students an opportunity to experiment
by entering various numbers; the displays connect geometric figures in simple artistic
forms; and the results for hexagons and octagons offer optical challenges. But the panel
can also give you an opportunity to explore with your class how the diagrams are drawn
and by this means to identify the roles of mathematics, programming and engineering in
the development of this kind of display. (It is important to note that we will be
developing an algorithm and not a program, although the two have obvious similarities.)
Here is a possible way you might do this.
1. Return to Panel 1.1.1 and give your students an opportunity to describe what is going on. Without looking again, what happens
when you enter 5 and press “Go.” What kind of figures, how many of them and how are they arrayed. Ask these questions for other entries,
say 7 and 20, and finally n. You might summarize with, “So the panel accepts the integer you enter and does all that work. I invite you
to explore this further with me.”
2. “It’s always a good idea to start with a simple case, so let’s see what happens when you run 4. To remind yourself of what is
happening, run 4 again and watch the resulting display carefully.” Then: “It looks as though the panel draws a path so let’s see how
that path goes. And to simplify our records, let’s assume that the turns are always to the left. (Thus a reversal would be 180° and a
right turn would be 270°.) And let’s call drawing the line segment, just s. Finally, we’ll just start by heading to the right.”
3. Now you can work out with your class drawing the first square: s,90°,s,90°,s,90°,s; drawing the square step by step.
4. Now ask what happens next. And have the students run n=4 to see that you turn 180°.
5. This will allow you to finish the steps for squares, n-4:
s,90°,s,90°,s,90°,s
180°
s,90°,s,90°,s,90°,s
180°
s,90°,s,90°,s,90°,s
180°
s,90°,s,90°,s,90°,s
6. Now try n=3 for equilateral triangles. And of course the key here is the size of that first turn, 120° Once you have that,
the steps for the first triangle are: s,120°,s,120°,s
7. Now students will need to run the panel again to see what the turn between triangles is. It is 240° (a right turn of 120°),
and with that you have the steps for 3:
s,120°,s,120°,s
240°
s,120°,s,120°,s
240°
s,120°,s,120°,s
Be sure you have both of these algorithms on display.
8. One more should give enough information to generalize.
Here are the steps using 5. Note that the key turns are the first and the one between pentagons.
s,72°,s,72°,s,72°,s,72°,s
144°
s,72°,s,72°,s,72°,s,72°,s
144°
s,72°,s,72°,s,72°,s,72°,s
144°
s,72°,s,72°,s,72°,s,72°,s
144°
s,72°,s,72°,s,72°,s,72°,s
9. Now you have enough to see what happens for any entered number, say n. To do this set out the three worked algorithms next to each other:
10. These can be summarized as (the extra turn at the end playing no role):
11. But we still have almost repetition within that repeated line. We can fix that by splitting the last turn into two parts:
12. Now we can split off that final turn to give us:
13. And this gives us our algorithm:
Repeat n times [(Repeat n times: s,360°/n),360°/n.]
14. This is, of course, still an oversimplification. I have omitted the initial direction and the length of s.
At this point your class should see how the algorithm that draws these complex diagrams works. But there is an additional
feature of what you have done. You can focus on the roles of math, programming and engineering. The math contribution centers
on the geometric relationship, 360°/n, and the development of the algorithm. The programming shares with math the algorithm
development and translates that algorithm into a series of commands dependent on the particular language involved. And the engineering
is the development of equipment that translates programming instructions into physical actions, in this case drawing the pictures
on your screen.
You may wish to point out to your students that this course is not about developing such algorithms and that they will not be
expected to develop such algorithms; rather, it is to provide them with, among many other things, some insights into what is going
on in the world of mathematics. The important aspect of what you will have done here is the involvement of your students in examining
this panel. You will, of course, have managed their progress, but you will have shown them an important fact: these well-disguised
magic tricks are really the result of careful thinking.