About Math

About Mathematics Commentary

Chapter 5. The Science of Secrecy

---

What this chapter is about

This chapter includes information about the history of secret communication, leading in the final sections to contemporary mathematical applications to this science.

Section Notes and Activities:

Section 5.1 compares messages that are physically hidden with those whose meaning is hidden but that can be examined openly. An example of the former is a note passed between friends in class. One example of the latter is a foreign language. To understand French, you must learn its key: a memorized French-English dictionary of word translations and some knowledge of French grammar. The remainder of the chapter deals only with the latter, but it differs from that example. In the rest of the chapter individual letters are what are translated into another form and communicated.

Some of this translation is not designed for secrecy but only to allow numerical devices to deal with non-numerical data. That is the basis for the ASCII Code table on page 97.

One way to consider with your students the difficulty of breaking secret codes is to consider the number of possible letter substitutions for a given word, “mathematics” for example. Even assuming that a given letter is replaced by the same new letter each time it occurs (a very substantial assumption as we will see) there are eight different letters to be replaced. That gives us 26⁸ > 208 billion possible words. (Even if you require that each letter is changed and no two are alike, you have 25• 24•23•22•21•20•19•18 > 43 billion possibilities.) This idea is extended and underscored in Section 5.2.

Sections 5.2 and 5.3 are both about substitution ciphers with the stress turning from methods of coding by formula to decoding substitution cypher messages by using clues taken from lengthy text passages. It is important that you make clear that the ciphers that involve specific shifts are only examples of substitution ciphers. If you fail to make this clear, some students will think that decoding substitution ciphers only involves determining the shift.

Section 5.2 introduces substitution ciphers with the Caesar shift. Once students understand that decoding an n-letter Caesar shift simply involves shifting 26 – n, you might discuss with your class how they would decode a message if they know that a message is a Caesar shift but they don’t know how far it is shifted. You could have them consider a phrase like:

Clearly trial and error will suffice. They need only enter the coded message in Panel 5.2.1 and try different shifts until they hit on the correct one. (In this case since 18 will decode the message, the original shift was 8.)

Section 5.3 discusses and illustrates literary and historical uses of substitution ciphers. These are related (distantly) to the general topic of stylometry, that may be of interest to your students. It is the “metry” (for measurement) in that word that makes stylometry mathematical: it is the study of literature or music or painting through statistical analysis. This subject considers such questions as: Who wrote individual Federalist Papers or the Book of Mormon? Did Shakespeare write or co-author plays in addition to those already recognized? Who was the main composer of each Beatles’ song? Did Rembrandt paint The Descent from the Cross that has long been attributed to him?

The central activity of this section, however, is decoding based on the analysis of extensive text passages. Whether you work through the passage from Poe’s short story, The Gold Bug, or assign it as homework, you might want to make copies for your students of the text with space allowed for them to fill in their translation. Below you will find that text for copying as well as the text for exercise (5.3.2) with the first six known letters identified:

---

---

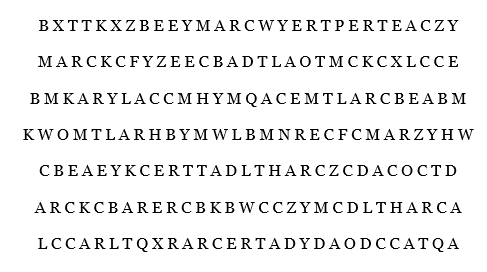
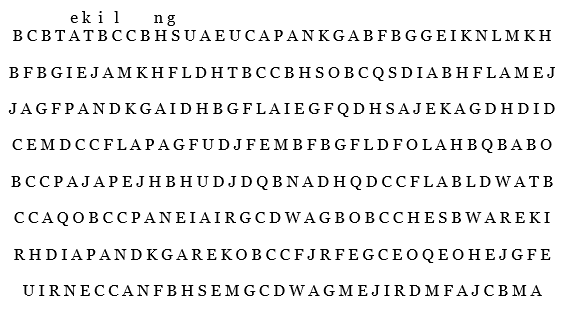
Section 5.4 is familiar to me from my own decoding messages during World War II. Many coded messages were sent in a form of de Vigenere code and each month when we were in port, I visited the shore base to pick up that month’s strips. To decode a message, I would choose strips whose leftmost letter was a letter of that day’s key word — like the FIVE of the example in the text. I would insert these in a metal board in the order FIVEFIVEFIVE…, as long as the incoming message. I would then simply line up the incoming letters in a vertical column. When that was done, the plain text message would appear in one of the other columns. I merely had to look for it.

I have described that process in order to indicate how complicated decoding a simple message was and how efficient are Panels 5.4.1 and 5.4.2 at carrying out this process. How I wish I had access to them 80 years ago. (You might want to tell some version of that story to impress your students with this simplification.)

Of interest, however, is the fact that I did have on my ship a coding machine for which I would obtain disks on those monthly shore visits. Using it to translate messages with higher priority was far easier. You merely set up the disks in a given order and “typed” the code letter by letter. The machine printed, instead of the letters you typed, the decoded text.

Section 5.5 extends the idea of the Caesar shift through use of modular arithmetic. Some students will have met modular arithmetic in their school math studies, but this will often be their first contact with a non-trivial application of this topic. It will play an important role through the remainder of this chapter, but again with the panels carrying almost all of the computational load.

As an extension of the calendar exercises (5.5.6), you might want to discuss with your class the reasoning behind the leap year rules. The U.S. Naval Observatory gives the following rules for leap years:

The earth completes a revolution around the sun in 365.2422 days. (This is called the tropical year.) With no adjustment for leap year, each calendar year would have 365 days and an error of .2422 days would accrue over time. The first level of correction is then to add a leap year once every four years, thus making the calendar year length 365.25 days. But now you are 365.25 – 365.2422 = 0.0078 days too long each year. That is why the next adjustment is made and in every 400 years you have 3 fewer leap years. With that adjustment we have 365.25 – 3/400 = 365.25 – .0075 = 365.2425 and the error is reduced to 365.2425 – 365.2422 = .0003 days. Thus we are still left with an error and over time that too will accumulate, but that error is very small: .0003 days per year = 26 seconds per year. It will take over three centuries for the Gregorian calendar to be a single full day off.

Section 5.6 presents the way the RSA code works, but with a very reduced example. For your students the complex procedure will simply involve copying a series of rather meaningless numbers. The important thing for them to see is that the key number, the product N = PQ, will be a very large number if P and Q are very large numbers. And the decoding process requires that N be factored to determine P and Q.

Clearly the point of this section is not to have students understand this process; rather, it is to have them see that messages can be sent by this complicated means. And they can do exactly that by means of Panels 5.6.1, 5.6.2 and 5.6.3.

The text mentions the fact that the RSA code presents a real problem to code breakers and this is worth discussing with your class. During World War II British and American mathematicians were able to break both the Japanese and German military codes. This gave them important tactical advantages. The result of this is summarized by Max Hastings in his book, Inferno: The World at War, 1939-1945 on pages 356-359. He concludes his summary with this passage:

Here is an opportunity to have your students consider a challenging question: whether unbreakable codes are good or bad. You could, for example, postulate that our country finds itself at war with country X and we are able to intercept many coded messages. Without the ability to decode these messages, we would find them worthless; but with them we would have the kind of advantage we had in World War II. This kind of discussion can change the government vs. RSA no longer the big guy vs. the little guys, but instead raises the question of national interest vs. people with “no stake in the game.”

Section 5.7 explains why factoring large numbers becomes time consuming. It is important to have your students understand that, although we informally refer to RSA as unbreakable, that is not really the case. It is simply that the time involved is too long to make the process practical.